- İnsanlık Neden Matematikle Başladı?
- Mezopotamya ve Mısır: Devletin Hafızası Olarak Matematik
- Antik Yunan: Özel Durumdan Genel Yasaya
- Hint Matematiği: Sıfır, Sonsuzluk ve Seriler
- Çin Matematiği: Pratik Hesap, Pi ve Alanlar
- İslam Dünyası ve Cebirin Doğuşu: Bilinmeyeni İsimlendirmek
- Newton, Leibniz ve Kalkülüs: Doğa Matematiğe Teslim Oluyor
- 19. Yüzyıl: Matematiğin En Soyut ve En Pratik Hâli
- 20. Yüzyıl: Einstein Konuşulur, Denklemler Unutulur
- Bilgisayar ve Yazılım Çağı: Matematik Görünmezleşiyor
- Yapay Zekâ: Lineer Cebiri Unutup “Model”e Tapmak
- Matematik Gerçekten Tahttan İndi mi?
- Sonuç: Sessiz Bir Doğa Yasası Gibi
Modern çağda artık kimse matematikçilerin adını manşetlerde görmüyor. Peki bu, matematiğin gerçekten sahneden çekildiği anlamına mı geliyor; yoksa matematik gücünü kaybetmeden sadece görünmez bir altyapıya mı dönüştü?
Son büyük matematikçinin kim olduğunu sorsak, bugün çoğumuzun aklına net bir isim bile gelmiyor. Uzman çevreler Grigori Perelman’dan, Andrew Wiles’tan, Terence Tao’dan söz ediyor; ama bu isimler geniş kitleler için Einstein ya da Newton kadar tanıdık değil. Fields Madalyası tartışmaları, çözülen dev teoremler, karmaşık ispatlar çoğu zaman sadece akademik odalarda ve dar haber başlıklarında kalıyor. Modern matematikçiler, çağımızın en karmaşık problemlerini çözüyor olsalar da, ders kitaplarının kenarına portreleri basılmış, herkesin çocukluk hafızasına kazınmış ortak figürler hâline henüz dönüşmüş değiller; Gauss, Euler ya da Newton gibi isimler hâlâ bu kolektif hafızanın son büyük yıldızları olarak yerini koruyor.
Ama sayfaları biraz çevirdiğimizde tuhaf bir boşluk hissi başlıyor. Sanki matematik sahnede rolünü oynayıp kulise çekilmiş; yerini fizikçilere, mühendislik dehalarına ve yapay zekâ girişimcilerine bırakmış gibi. Modern çağda matematik, rolünü başarıyla tamamlayıp geri plana çekilmiş, işini hâlâ sessizce sürdüren bir doğa yasası gibi çalışıyor.
Bugün matematik neden bu kadar az konuşuluyor? Acaba önceki kuşak matematikçiler gerçekten ‘her şeyi’ çözdü de sıra sadece uygulamaya mı kaldı, yoksa matematik görünmez bir çekirdeğe dönüşüp tüm bilimlerin içinde kaybolduğu için mi onu fark etmiyoruz?
Bugünün manşetlerinde fizikçileri, biyoteknoloji girişimcilerini, yapay zekâ kurucularını görüyoruz. Matematikçiler ise sahnenin gerisinde, kodların, denklemlerin ve modellerin içinde kaybolmuş durumda. Bu, matematiğin önemini kaybettiği anlamına gelmiyor; tam tersine, matematik bugün kimyanın, fiziğin, ekonominin ve yazılımın içine gömülmüş, tüm bilimlerin görünmez işletim sistemi haline gelmiş durumda.
Peki insanlık neden bilime matematikle başladı? Matematik nasıl tüm disiplinlerin çekirdeğine yerleşti? Ve bugün neden adını daha az duysak da hâlâ en yüksek öneme sahip?
İnsanlık Neden Matematikle Başladı?
İlk bakışta iddialı gelebilir ama insanlık, bilime matematikle başladı. Bunun nedeni soyut düşünceye duyulan özel bir sevgi değil; çok daha basit ve acil bir ihtiyaçtı: Hayatta kalmak.
Tarımın ilk ortaya çıktığı dönemlerde iki soru, neredeyse her şeyden önemliydi:
- Kaç? Kaç koyun, kaç çuval buğday, kaç işçi, kaç gün?
- Ne zaman? Ne zaman ekilecek, ne zaman taşacak, ne zaman sel basar, ne zaman hasat yapılacak?
Dil, “kim, ne, neden?” sorularını çözer. Matematik ise “ne kadar, ne sıklıkla, ne zaman?” sorularını. Bu yüzden sayılar ve ölçüler, felsefeden önce; geometri, soyut sanattan çok önce hayatımıza girdi.
İnsanlar, önce tarladaki ürünü, ahırdaki hayvanı ve gökyüzündeki döngüyü saymak zorunda kaldı. Matematik, bu yüzden doğrudan hayatta kalma refleksinin içine yerleşti: Bir anlamda ilk bilimsel dil, matematikti.
Mezopotamya ve Mısır: Devletin Hafızası Olarak Matematik
Tarih sahnesinde ilk büyük matematik sıçraması, bugünkü Irak, Suriye, Mısır hattında belirdi.
Mezopotamya’da kil tabletlerin üzerine kazınan çiviyazıları, romantik hikâyelerden çok borç, vergi ve stok kayıtlarını içeriyordu. Tahıl ambarları, işçi listeleri, vergi oranları… Yani matematik, en başta bir “soyut sanat” değil; devletin ve pazarın hafızasıydı.
Mısır’da Nil nehrinin taşma döngüsü, tarımın bütün ritmini belirliyordu. Nehir her yıl yatağından taşarak tarlaları hem bereketli hem de belirsiz hale getiriyordu. Bu dalgalanmayı kontrol etmek için bir tür takvim matematiği gelişti. Yıldızların konumu, Ay’ın evreleri ve nehir seviyesi birlikte takip edildi; “ne zaman ekelim, ne zaman bekleyelim?” sorusuna gökyüzü üzerinden cevap arandı.
Sel sularının her yıl arazi sınırlarını silip süpürmesi, insanları bir başka matematik türüne zorladı: Geometri. Toprak yeniden bölüşülecekse, kim ne kadar alacak? Tarla sınırı nereden geçiyor?
Bu dönemi temsil eden isimler çoğu zaman anonim “Babil kâtipleri” olarak karşımıza çıksa da, örneğin Ahmes (Ahmose) adlı Mısırlı yazıcı, Rhind Matematik Papirüsü’nü kopyalarken dönemin problem çözme kültürünü kayda geçirdi. Erken Mısır geleneğinde mimar, hekim ve hesapçı kimlikleriyle anılan İmhotep gibi figürler, pratik geometri ve ölçüm bilgisini anıtsal yapılara taşıdı.
Böylece matematik, üç temel alanda aynı anda büyümeye başladı:
- Sayılar → Sayma, toplama, çıkarma; yani muhasebe.
- Zaman → Takvim, mevsimler, ekim-biçim döngüleri.
- Alan → Toprak ölçme, sınır çizme, ilk geometrik düşünceler.
Henüz ortada “bilim insanı” yoktu; ama rakamları ve şekilleri kullanarak dünyayı idare etmeye çalışan büyük bir uygarlık deneyi vardı.
Antik Yunan: Özel Durumdan Genel Yasaya
Matematiğin gerçek anlamda “bilim dili”ne dönüşmesi, Antik Yunan’da başladı.
Mezopotamyalı ve Mısırlı kâtipler, belirli problemlere pratik çözümler üretiyordu. Yunan matematikçileri ise ilk kez şu soruyu sordular:
“Sadece bu üçgen için değil, bütün üçgenler için ne söyleyebiliriz?”
Bu soru, insan düşüncesinde devrimsel bir adımdı. Artık amaç, yalnızca belli bir tarlanın alanını hesaplamak değildi; “her üçgenin iç açılarının toplamı nedir?” gibi evrensel ve soyut bir soruya cevap aranmaya başlandı.
- Thales, basit görünen ama genellenebilir geometrik ilişkilerle “ispat” fikrini tohumladı.
- Pisagor, belirli bir dik üçgenin kenarlarını değil, bütün dik üçgenleri ilgilendiren bir ilişkiyi formüle etti.
- Öklid, Elemanlar adlı eseriyle geometriyi tek tek problemlerden değil, aksiyomlardan başlayarak inşa etmeye çalıştı.
- Arşimet, alan ve hacim hesaplarıyla, henüz adı konmamış bir analiz düşüncesini sezgisel olarak kullandı.
Böylece matematik, ilk kez “tek tek vakalar için çözüm üreten araç” olmaktan çıkıp, genel yasalar üreten bir zihin alışkanlığı haline geldi. Bu alışkanlık, fizik dâhil bütün bilimlere yayılacak bir model sundu: Önce tanımlar, sonra aksiyomlar, sonra ispat.
Matematik, bu dönemde yalnızca sayıların, açıların değil; düşünmenin yöntemi haline geldi.

Hint Matematiği: Sıfır, Sonsuzluk ve Seriler
Antik Yunan’la paralel ve sonrasında, Hindistan’da da güçlü bir matematik geleneği gelişti. Bu gelenek, bugün hâlâ kullandığımız pek çok temel kavramın derinleşmesinde rol oynadı.
- Aryabhata, trigonometrik fonksiyonlara benzeyen hesaplar yaparak astronomiyi sayısal bir zemine taşıdı, π için oldukça iyi bir yaklaşım elde etti.
- Brahmagupta, negatif sayılar ve sıfırla ilgili kuralları daha sistemli hale getirdi; denklemler üzerinde çalışarak cebirin gelişimine katkı verdi.
- Bhaskara II, denklemler ve seri fikirleriyle, analiz öncesi “değişim” kavramına dokunan çözümler üretti.
Hint matematiği, özellikle sıfırın ve onluk sistemin olgunlaşmasında belirleyiciydi; bu miras, İslam dünyası üzerinden Avrupa’ya taşınarak hesap yapma biçimimizi kökten değiştirdi.
Çin Matematiği: Pratik Hesap, Pi ve Alanlar
Aynı yüzyıllarda Çin’de de, çoğu pratik ihtiyaçtan doğan ancak derinlikli yöntemler içeren bir matematik kültürü ortaya çıktı.
- Liu Hui, geometrik yöntemlerle alan ve hacim hesaplarını geliştirdi; çokgenlerle π’yi yaklaşık olarak bulmaya çalıştı.
- Zu Chongzhi, π için inanılmaz hassas bir yaklaşım elde etti ve astronomiyle birlikte çalıştı.
Dokuz Bölümlü Matematik Sanatı gibi metinler, vergi, arazi bölüşümü, mühendislik ve su kanalları için gereken hesapları sistematik hale getiriyordu. Çin matematiği, soyuttan çok pratiğe dönük görünse de, kullandığı teknikler daha sonra modern matematik açısından da ilham verici sayılacak bir ayrıntı zenginliği taşıyordu.
İslam Dünyası ve Cebirin Doğuşu: Bilinmeyeni İsimlendirmek
Orta Çağ boyunca matematik hikâyesinin ağırlık merkezi, Akdeniz’in güney ve doğu kıyılarına kaydı. Bağdat, Şam, Kurtuba, Buhara gibi şehirler, hem çeviri hem de özgün üretim merkezlerine dönüştü.
Bu dönemin en önemli katkılarından biri, adını bugün hâlâ kullandığımız bir alan: cebir (al-jabr). Muhammed el-Harezmi, cebiri sistemleştiren eserleriyle hem denklemlerin çözümünde yeni yollar açtı hem de ismi “algoritma” kelimesine kaynak oldu. Ömer Hayyam, üçüncü dereceden denklemleri geometrik yöntemlerle sınıflandırdı; takvim ve astronomi çalışmalarıyla matematiği gökyüzüne bağladı. el-Biruni ve Nasirüddin Tusi gibi isimler, trigonometrinin bağımsız bir disiplin haline gelmesinde, ölçüm ve astronomik hesapların hassaslaşmasında rol oynadı.
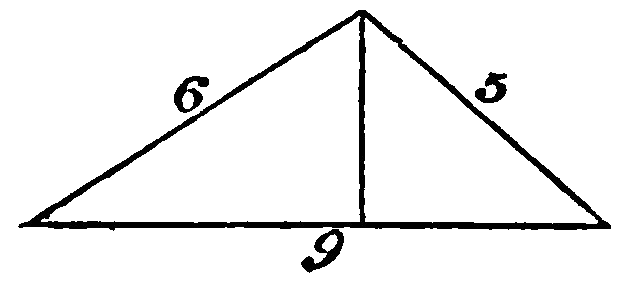
Kaynak: Wikimedia Commons, “The Algebra of Mohammed Ben Musa – page 82b”.
Cebirin doğuşu, “bilinmeyeni adlandırma” cesaretiydi. Somut rakamlar yerine, “x” ve “y” gibi soyut sembollerle problem kurmak ve çözmek mümkündü.
Bu dönüşüm şu açıdan çok önemliydi:
- Matematik ilk kez, somut nesnelerden tamamen bağımsız bir problem kurma diline kavuştu.
- Bilinmeyeni sembolleştirerek yönetmek; sadece ticaretin değil, ileride fiziğin, ekonominin ve bilgisayar bilimlerinin temel refleksi olacaktı.
Aynı dönemde Hint rakamlarının ve “0” kavramının İslam dünyası üzerinden Batı’ya taşınması, hesap yapmayı inanılmaz derecede hızlandırdı.
Artık denklemler kurulabiliyor, bilinmeyenler yönetilebiliyor, daha karmaşık ilişkiler çözülüp kaydedilebiliyordu. Matematik, ticaretin ve astronominin ötesine geçip, soyut problem çözme sanatına dönüştü.
Newton, Leibniz ve Kalkülüs: Doğa Matematiğe Teslim Oluyor
17. yüzyılda sahneye çıkan Isaac Newton ve Gottfried Wilhelm Leibniz, sadece yeni formüller icat etmedi; doğaya bakmanın şeklini kalıcı olarak değiştirdi.
Türev ve integral, yani kalkülüs dediğimiz yapı, hareket eden her şeyin matematikle ifade edilmesini mümkün kıldı:
- Bir cismin hızı nasıl değişiyor?
- Bir gezegenin yörüngesi nasıl hesaplanır?
- Hangi kuvvet hangi sonucu doğurur?
Artık fizik, “sözel yasalarla” değil; denklemlerle yazılıyordu. Matematik, doğanın diline tamamen nüfuz etti. Hareket, çekim, ışık… Hepsi birer fonksiyon ve diferansiyel denklem haline geldi.
Bu noktadan sonra şu fikri ciddiye almak zorundaydık:
“Eğer bir şeyi matematiksel olarak modelleyebiliyorsak, onu gerçekten anlamaya başlamışız demektir.”
Bilim tarihinde ilk kez, doğa “yaklaşık açıklamalarla” değil, net formüllerle ifade edilebilen bir sistem olarak düşünülmeye başlandı. Matematik, sadece destek rolünde değil; fiziğin bizzat omurgası haline geldi.
19. Yüzyıl: Matematiğin En Soyut ve En Pratik Hâli
18. ve 19. yüzyıllar boyunca matematik iki farklı yöne birden büyüdü:
- Bir yanda son derece pratik alanlar:
- Elektrik ve manyetizmayı birleştiren denklemler,
- Buhar makineleri, köprüler, demiryolları için yapılan mühendislik hesapları,
- Olasılık teorisinin sigortacılık ve finansla buluşması…
- Diğer yanda son derece soyut alanlar:
- Sonsuz kümeler, yeni geometri türleri, sayı teorisinin derin katmanları,
- “Gerçek” dünyada doğrudan karşılığı olmayan ama ileride bilgisayar biliminin ve kriptografinin temeli olacak yapılar.
Bu dönemde Leonhard Euler, neredeyse her alt alana dokunan üretkenliğiyle modern matematiğin temel taşlarını döşedi. Carl Friedrich Gauss, sayı teorisinden istatistiğe, manyetizmadan astronomiye uzanan katkılarıyla “matematikçilerin prensi” diye anıldı. Bernhard Riemann, hem analizde hem de farklı geometri türlerinde yaptığı çalışmalarla, ileride görelilik teorisinin ve modern topolojinin önünü açtı.
Matematik, bir yandan fizik ve mühendisliğin dili haline gelirken, diğer yandan kendi başına bir soyut evren kuruyordu. Bu soyut evrenin kahramanları, bugün hâlâ kitaplarda adı geçen Gauss, Riemann, Cantor ve daha niceleriydi.
Ama aynı dönemde kamuoyu algısı yavaş yavaş değişmeye başladı. Sanayi devrimi, şehirlerin büyümesi, makinelerin hayatı doldurmasıyla birlikte, sahneye yeni karakterler çıktı: mühendisler ve fizikçiler. Matematik, onların arka planda kullandığı araç gibi görünmeye başladı.
20. Yüzyıl: Einstein Konuşulur, Denklemler Unutulur
20. yüzyıl, matematiğin hem zirveye çıktığı hem de görünürlüğünü kaybetmeye başladığı bir dönem oldu.
Görelilik teorisi, kuantum mekaniği, istatistik devrimi, oyun teorisi, bilgi teorisi… Bunların her biri, yoğun matematiksel yapılar olmadan var olamazdı. Ancak kamuoyunun hafızasında kalan, çoğunlukla kişiler ve hikâyeler oldu: Einstein’ın saçı, Oppenheimer’ın cümleleri, “kuantum” kelimesinin etrafındaki esrar.
Oysa bu yüzyılın zeminini hazırlayan isimler arasında, matematiği içerden dönüştüren figürler vardı:
- David Hilbert, ortaya koyduğu 23 problemle 20. yüzyıl matematiğine bir gündem sundu.
- Kurt Gödel, eksiklik teoremleriyle, “her şeyi ispatlayan tam bir sistem” hayalini matematiğin içinden kırdı.
- Emmy Noether, soyut cebir ve simetri çalışmalarıyla, modern fiziğin en derin yasalarından birine (Noether teoremi) adını verdi.
Matematikçiler, bu büyük dönüşümün tam ortasında çalıştılar; ancak isimleri, çoğu zaman fizikçilerin gölgesinde kaldı. Yine de matematik olmadan:
- Enerji–kütle ilişkisi yazılamaz,
- Atom çekirdeği modellenemez,
- Radyoaktif bozunma istatistiksel olarak anlaşılamazdı.
Matematik, farkında olmadan bilimsel prestiji paylaştıran bir disipline dönüştü: Kendisi perde arkasında kaldı, sahneyi fizik ve kimya bölüştü.
Bilgisayar ve Yazılım Çağı: Matematik Görünmezleşiyor
20. yüzyılın ikinci yarısından itibaren matematik, yepyeni bir bedenin içine taşındı: bilgisayarlar.
Bir bilgisayarın en temelinde, tamamen matematiksel yapılar vardır:
- Boolean mantık (doğru–yanlış),
- Sayı sistemleri (ikilik, onaltılık),
- Algoritmalar (adım adım çözüm yöntemleri).
Ama günlük hayatta kimse bilgisayarına bakıp “şu anda çok yoğun bir matematik çalışıyor” diye düşünmez. Ekranda gördüğümüz şey, bir fotoğraf düzenleme programı, bir oyun, bir bankacılık uygulaması ya da sosyal medya akışıdır.
İşin ilginci, çocuklara “kodlama” eğitimi veriyoruz; ama çoğu zaman onlara aslında uygulamalı matematik öğrettiğimizi söylemiyoruz. Döngüler, koşullar, fonksiyonlar… Bunların hepsi, matematiğin programlama diline çevrilmiş hâli.
Matematik, bu çağda sahneyi tamamen yeni karakterlere bıraktı:
- “Yazılımcı”,
- “Veri bilimci”,
- “Yapay zekâ mühendisi”.
Etiket değişti, ama altyapı aynı kaldı.
Yapay Zekâ: Lineer Cebiri Unutup “Model”e Tapmak
Bugün yapay zekâ, çağımızın en parlak vitrini. “Model eğitmek”, “parametre sayısı”, “yüz tanıma”, “büyük dil modeli” gibi kavramlar günlük dile kadar sızdı.
Ama bu sistemlerin kalbinde ne var?
- Lineer cebir: Devasa boyutlu matrisler ve vektörler,
- Türev ve integral: Geri yayılım (backpropagation) denilen öğrenme süreci,
- İstatistik ve olasılık: Belirsizliğin ve hata payının yönetilmesi.
Yani yapay zekâ dediğimiz şey, son derece yoğun bir matematiksel altyapının, görsel olarak cazip ve ticari olarak paketlenmiş hâli.
Biz “AI” diyoruz, ama gerçekte konuştuğumuz şey, matematiğin bilgisayarlardaki en yeni kılığından başka bir şey değil.
Bu noktada ilginç bir paradoks oluşuyor:
- Matematik hiç olmadığı kadar güçlü: Her sektörde, her modelde, her hesapta.
- Matematikçiler hiç olmadığı kadar görünmez: Markanın ön yüzünde yazılımcı, girişimci, CEO var; denklem tasarlayan insanlar değil.
Matematik Gerçekten Tahttan İndi mi?
Tarihsel çizgiye uzaktan baktığımızda şu tabloyu görüyoruz:
- Başlangıçta matematik, insanlığın hayatta kalmak için kullandığı tek soyut dildi.
- Tarım, ticaret, takvim, ilk devletler → Hepsi matematik olmadan düşünülemezdi.
- Zamanla fizik, kimya, biyoloji, ekonomi, sosyoloji gibi alanlar ortaya çıktı.
- Bu disiplinler büyüdükçe, matematik onların içindeki ortak altyapıya dönüştü.
Popüler kültür, sahnedeki oyun değiştikçe yeni kahramanlar seçti: Galileo, Darwin, Einstein, bugün de yapay zekâ kurucuları… Matematik ise yavaş yavaş özel isimlerden çıkıp, arkaplandaki bir prensibe benzedi.
Elektrik hakkında düşün: Bir zamanlar yeni ve büyüleyici bir keşifti, herkes ondan konuşuyordu. Bugün evdeki lambayı açarken elektriği fark etmiyoruz bile; hayatın varsayılan parçası haline geldi. Matematik de benzer bir dönüşüm geçiriyor: Merak edilen bir “alan” olmaktan çok, her şeyin üzerinde çalıştığı altyapı haline geliyor.
Bu yüzden:
Matematik geri çekilmiş gibi görünüyor; çünkü beden büyüdükçe, iskelet görünmez hale geliyor.
Sonuç: Sessiz Bir Doğa Yasası Gibi
Artık kimse günlük hayatta “matematikçinin yeni teoremini” tartışmıyor. Sosyal medyada bir matematikçinin hayat hikâyesi, bir girişimcinin yatırım turu kadar ilgi görmüyor. Ders kitaplarına adını kazımış son büyük matematikçi nesiller öncesinde kalmış gibi.
Ama bu, matematiğin görevini tamamlayıp kenara çekildiği anlamına gelmiyor. Tam tersine, matematik bugün:
- Tarım verimliliğini,
- İklim modellerini,
- Finans piyasalarını,
- Trafik akışını,
- Hastalık yayılımını,
- Yapay zekâ sistemlerini
hesaplayan, modelleyen, sınırlarını çizen sessiz motor.
Modern çağda matematik, rolünü sahnenin ortasında oynamış ve şimdi geri planda, işini hâlâ sessizce sürdüren bir doğa yasasına dönüşmüş gibi. Adı daha az anılıyor olabilir; ama dünyayı anlamak ve değiştirmek için hâlâ elimizdeki en keskin, en güvenilir dil o.
İnsanlık bilime matematikle başladı. Görünen o ki, bilimin son satırı yazılacaksa, o satırda da yine bir şekilde bir denklem olacak.
Kaynaklar ve Önerilen Okumalar
- Ian Stewart – Galois’ten Gödel’e: Matematiğin Kısa Tarihi
- Morris Kline – Matematiğin Kaybolan Görkemi (Mathematics: The Loss of Certainty)
- Carl B. Boyer & Uta C. Merzbach – A History of Mathematics
- Victor J. Katz – A History of Mathematics: An Introduction
- Amir D. Aczel – The Mystery of the Aleph (sonsuzluk ve Cantor üzerine)
- Jim Al-Khalili – İslam Bilimi’nin Altın Çağı (İslam matematik geleneği için)





